Elle peut paraitre effrayant en premier lieu, mais avec une IPP tabulaire, ce n'est rien de réellement compliqué.
On vas d'abord placer x² dans la colonne D car il s'agit du terme à droite (donc à coté de dx).
On vas ensuite poser 3x+2 dans la colonne I car il s'agit du terme à gauche (donc éloigné de dx).
Dans notre tableau, D signifie "dériver" et I "intégrer".
En signe, nous allons osciller entre + et - de façon périodique. En ligne 1 on aura le signe + et en ligne 2 le signe - avant d'avoir de nouveau en ligne 3 le signe +.
Soit, pour simplifier, si le numéro de la ligne est pair alors le signe est négatif. Si le numéro de la ligne est impair, alors le signe est positif.
D'où, on vas après les avoir placés dans le tableau, dériver successivement le terme dans la colonne D et intégrer successivement le terme dans la colonne I.
On s'arrêtera quand la dérivée sera nulle ou qu'on sera de retour à l'expression initiale de la dérivée (période).
D'où, l'on obtient ce tableau :
On s'arrête pour 0 dans la colonne D dans notre processus. Cela, avant d'additionner les produits D*I de la façon suivante en prenant en compte du signe dans la colonne signe comme signe associé au produit.
On aura ainsi à faire : x²*((3x²)/2+2x)-2x*((x^3)/2+x²)+2*((x^4)/8+(x^3)/3)-0∫(x^4)/8+(x^3)/3
Or, l'intégrale s'annule car multipliée par 0. Cela rend la tâche plus facile car dès alors on a :
3(x^4)/2+2(x^3)-(x^4)-2(x^3)+2(x^4)/8+2(x^3)/3=3(x^4)/2-(x^4)+(x^4)/4+2(x^3)/3
On factorise par x^4 et x^3 :
x^4(3/2-1+1/4)+2(x^3)/3=3(x^4)/4 + 2(x^3)/3 + C
Ainsi, l'intégrale est résolue !
Cette méthode peut permettre de gagner du temps sur certaines intégrales, dont celles avec des cosinus ou des sinus. Elle est utile, et permet d'éviter à passer par l'IPP.
Personnellement, je l'ai trouvé plus intuitive et plus facile à utiliser. Elle est plus facile à retenir, et ne demande pas de formule mais simplement de faire un tableau et de procéder par opérations.
Il s'agit d'une méthode qui peut vous être utile, notamment pour certaines intégrales où vous voulez évitez de passer par une IPP pour gagner du temps.
B) La propriété du roi.
Oui, nom étonnant n'est-ce pas ? Pourtant, cette propriété a tout de royal.
Je vous la présente :
Qu'est-ce que cette propriété nous dit ?
Simplement, elle nous dit que c'est EXACTEMENT la même chose d'intégrer de gauche à droite que de droite à gauche car intégrer concrètement c'est calculer l'aire sous la courbe.
De plus, cette propriété nous permet de résoudre des intégrales très difficiles, et est donc d'une importance maximale.
Parmi toutes celles ici, il s'agit de l'une de celles à retenir en priorité.
Nous pouvons notamment l'utiliser sur des fonctions trigonométriques pour les intégrer, là où ça devient très difficile.
On a ainsi, de nouvelles propriétés pour intégrer. Celles-ci vont nous simplifier la vie mais aussi nous permettre d'optimiser le temps nécessaire à calculer.
Prenons un exemple simple :
On peut directement résoudre, cette intégrale est évidente mais elle servira à montrer que la propriété marche.
On a, selon la propriété du roi, en posant f(x)=x².
On a donc en séparant la somme en trois intégrales dont on fait la somme :
Soyons honnête, on est de retours au point zéro...
Or, nous pouvons faire une somme pour trouver la solution :
On peut vérifier si ce résultat est égal à celui obtenu en intégrant simplement x² avec sa primitive.
F(x)=(x^3)/3
D'où :
F(1)=(1^3)/3=1/3
F(3)=(3^3)/3=9
Or, F(3)-F(1)=9-1/3=27/3 - 1/3 = 26/3.
On obtient le même résultat, la propriété du roi fonctionne donc bien !
Ici, notre exemple était pas très approprié, en vu de sa simplicité mais il montre bien que l'on peut utiliser la propriété du roi pour trouver une intégrale.
Elle apparait notamment dans les concours d'intégration. On peut penser au concours américain "integration bee 2000" où il y'avait un exercice qui la nécessitait bien qu'il était extrêmement compliqué. Plus largement, cette propriété peut s'avérer utile dans plein de cas où on a des intégrales qui paraissent compliquées et d'apparence impossible, mais qu'on peut résoudre avec.
C) Intégration par changement de variable.
Il est peu probable que vous ayez déjà intégré ainsi au lycée, or cette méthode est aussi utile. Elle consiste à prendre un terme et à poser un terme u égal à celui-ci puis d'intégrer u et à partir du résultat de l'intégration on aura le résultat de l'intégrale.
Prenons un exemple :
Cette intégrale bien qu'inquiétante, peut en réalité facilement être simplifiée.
On vas poser u=g(x).
On vas essayer d'exprimer l'intégrale selon u.
On sait que g'(x) est la dérivée de u. D'où on va poser du (dérivée selon u) tel que du=g(x)dx.
Ainsi, l'on a :
Déjà, ça inquiète moins ! Cependant... on vas où à partir d'ici ? Car oui c'est bien de transformer un chemin en voiture compliqué à un chemin en voiture moins compliqué, mais si on ne sait pas conduire... on arrive nulle part !
Eh bien, moi je dis qu'il n'y a rien de mieux qu'un exemple pour permettre au cerveau d'appréhender et pour vous apprendre à conduire sur la route des primitives !
Prenons cet intégrale :
Ainsi, on pose u=x^2, alors u'=2x. D'où, l'on pose du=2x*dx.
On a donc :
Ce qu'il y'a de bien avec cette méthode c'est non seulement sa capacité à résoudre des intégrales, mais aussi ici le temps en lequel elle peut le faire. On a fait que trois étapes ici :
-On a substitué par u.
-On a intégré.
-On a résolu en écrivant u=x².
Elle est rapide, utile et efficace et permet de traiter des intégrales plus complexes en la combinant à d'autres méthodes.
D) Intégration par décomposition.
Une méthode assez utile, qui est liée à la décomposition de polynômes du second degrés en espèces.
On a deux polynômes P(X) et Q(x). On a aussi deg(P)<deg(Q), deg étant le degré du polynôme.
On voudra alors calculer l'intégrale de P(x)/Q(x).
Alors attention, soyez attentifs pour bien comprendre la méthode jusqu'au bout :
On a, imaginons l'intégrale de deux polynômes, soit :
On va d'abord commencer par factoriser le dénominateur, ce qui nous donnera x²-x-2=(x-2)(x+1).
Dès alors, on va décomposer la fraction en espèces (en parties distinctes) :
Soit, pour déterminer les valeurs de A et B on va procéder ainsi.
D'où l'on peut multiplier les deux cotés par (x-2)(x+1) et on a ainsi :
Soit, 2x+3=Ax+A+Bx-2B, ainsi on a : Ax+Bx+A-2B=2x+3 soit x(A+B)+A-2B=2x+3
Or, A et B sont des entiers en vu de la décomposition en fraction, ainsi :
x(A+B)=2x si et seulement si A+B=2 d'où on a qu'un seul couple d'entiers naturels vérifiant cela : A=1 et B=1.
Ainsi, l'on a les solutions : A=B=1.
D'où, on a facilement :
Une méthode utile pour les intégrales avec des fractions et des polynômes.
E) Linéarité.
Cette propriété est très utile. On va la poser puis l'expliquer.
Simplement, si on a deux fonctions f(x) et g(x), dont on veut la somme on peut les "séparer" en deux intégrales que l'on traite individuellement avant de les additionner. Si on a deux réels, alpha et beta qui sont coefficients des fonctions, ils deviennent coefficients des intégrales. Elle est assez utile, notamment car elle permet d'éviter de calculer l'intégrale de la somme mais seulement deux plus petites intégrales...
D'où l'on déduit :
Ainsi, on a deux propriétés qui seront plutôt utiles pour intégrer.
F) Relation de Chasles
Tiens, ce nom vous dit quelque chose ? Eh bien, figurez vous que il vient de la ressemblance entre la prochaine propriété et la relation de Chasles.
Cette propriété, nous dit que si il y'a un réel c compris entre a et b alors pour intégrer de a à b on peut simplement faire la somme de l'intégrale de a à c et de celle de c à b.
Il suffit de voir ça graphiquement :
Comme vous pouvez le voir, en représentant avec Scipy, numpy et matplotlib on trouve que l'aire sous la courbe peut être divisée en deux. Par l'aire de a à b et de b à c. D'où en faisant la somme des deux on aura l'aire totale sous la courbe qui est l'intégrale de a à c. Plus largement sachant que b est compris entre a à c, et que on fait la somme de l'intégrale de a à b et de b à c alors on fait la somme des aires sous les courbes entre les deux intégrales.
C'est comme si vous marchiez sur une montagne et que vous vous arrêtiez en un point, et que ensuite vous continuez pour arriver au sommet. Vous finissez au sommet même après vous être arrêté, vous avez juste divisé le chemin en deux parties.
II - Les formules indispensables !
Vous vous souvenez certainement du tableau des primitives... eh bien il est temps de l'étendre (enfin...) ! Et ainsi, d'apprendre les opérations sur les intégrales et de nouvelles primitives pour intégrer. Un rappel ne fait aussi pas de mal sur les primitives vues au lycée.
III - Les nouvelles propriétés.
A) Convergence d'une intégrale et propriétés variées !
Cher lecteur, vous vous souvenez certainement des propriétés liés à la convergence des suites et des fonctions... eh bien, vous êtes gâtés car une intégrale peut aussi converger !
Reste à déterminer dans quel cas.
On pose immédiatement cette belle propriété :
Soit, cela se résume à déterminer la limite quand b tend vers l'infini (+infini ou -infini) pour la fonction F(x) primitive de f(x).
On va poser le critère qui permet de dire si une fonction est intégrable ou pas.
Une fonction f admet une intégrale de a à x sur un intervalle I si et seulement si :
-a appartient à ce même intervalle I.
-f est continue sur cet intervalle I.
-F appartient à I et la primitive de f s'annule en a.
Si une de ces trois propriétés n'est pas vérifié, notre fonction n'est pas intégrable.
Aussi, vous vous souvenez du théorème des gendarmes, eh bien il y'a son équivalent pour les intégrales ! Même si ce n'est pas la même chose...
Je vous présente le critère de comparaison :
Si :
Il fonctionne si l'on a deux fonctions g(x) et f(x) tels que : 0 ≤ f(x) ≤ g(x) sur [a ; + ∞ [ Or le critère dit aussi :
Ces propriétés sont particulièrement utiles à retenir, elles permettront de faire des raccourcis et d'aller beaucoup plus vite par exemple face à une suite d'exercices sur les intégrales.
Je me permet de finir cet article en beauté, avec un dernier lemme : le lemme d'Abel.
Soit f(x) et g(x) deux fonctions telles que elles soient continues sur un intervalle [a ; +∞ [ avec a un réel.
Alors, on a un réel M tel que :
Et tel que :
Ainsi, je pense qu'à partir de cet article, vous êtes lourdement armés pour faire face aux intégrales, vous avez désormais un vrai arsenal de méthodes et de propriétés qui peuvent vous simplifier le travail à réaliser ! Or, je n'ai pas abordé le thème des fonctions trigonométriques hyperboliques, je préfère le garder pour un prochain article où l'on va les approfondir et voir leurs propriétés en profondeur. En attendant, vous possédez un bagage réel désormais.
J'espère que mon article a su vous aider.
-DAOUADI Zine-Eddine.
Cet article est mis à votre disposition sous la licence Creative Commons Attribution 4.0 International (CC BY 4.0).














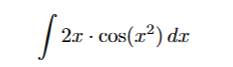


















Commentaires
Enregistrer un commentaire